KESEIMBANGAN PARTIKEL

Suatu partikel disebut dalam keadaan seimbang, bila jumlah aljabar gaya-gaya yang bekerja pada partikel tersebut nol.
Syarat keseimbangan partikel adalah : F = 0
Jika partikel terletak pada bidang XY maka syarat keseimbangan : FX = 0 dan FY = 0

Partikel merupakan ukuran benda terkecil, sehingga sering digambarkan sebagai titik. Akibatnya, jika ada gaya yang bekerja pada partikel, maka gaya tepat mengenai pada pusat massa benda. Oleh karena itu, partikel hanya mengalami gerak translasi (menggeser). Gerak translasi merupakan gerak yang memenuhi hukum II Newton.
Jika partikel terletak pada bidang XY dan gaya-gaya yang bekerja diuraikan alam komponen sumbu X dan sumbu Y, maka syarat kesetimbangan partikel. lesaikannya, Anda dapat menggunakan syarat keseimbangan. Secara sederhana Anda juga dapat menggunakan aturan sinus dalam segitiga. Gerak Rotasi Gerak rotasi (melingkar) adalah gerakan pada bidang datar yang lintasannya berupa lingkaran.

Titik Berat

Semua benda di bumi mempunyai berat. Berat suatu benda dapat dianggap terkonsentrasi pada satu titik yang di sebut pusat gravitasi atau titik berat. Pada titik berat ini gaya-gaya yang bekerja menghasilkan momen resultan sama dengan nol. Karena itulah benda yang di tumpu pada titik beratnya akan berada dalam keseimbangan statik. Dengan kata lain titik berat adalah titik tangkap dari semua gaya yang bekerja. Contoh berikut ini menunjukkan bagaimana menentukan letak resultan gaya yang sejajar.

Contoh soal

Empat buah gaya masing-masing F₁ = 20N, F₂ = 30N, F₃ = 40N dan F₄ = 10N bekerja pada sepanjang sumbu x seperti gambar berikut. Tentukanlah letak resultan keempat gaya tersebut!

Jawab:
gaya F₁= 20 N dengan x₁=-1m
gaya F₂=30 N dengan x₂=1m
gaya F₃=40 N dengan x₃=2m
gaya F₄= 10 N dengan x₄=3m

Letak Resultan keempat gaya tersebut dapat di tentukan dengan persamaan

Nah setelah mempelajari bagaimana mencari letak resultan gaya sejajar yang bekerja pada benda marilah kita lihat bagaimana letak resultan gaya yang bekerja pada sebuah benda homogen berbentuk tak beraturan berikut ini.

Benda dengan berat w tersusun atas partikel-partikel dengan berat w₁, w₂, w₃, .... yang terletak pada koordinat (x₁,y₂,z₃), (x₂,y₂,z₂), (x₃,y₃,z₃) dan seterusnya...    

letak titik resultan gaya-gaya tersebut  secara umum dapat ditentukan dengan persamaan

	w1= w2= w3= berat masing-masing partikel X1 = letak partikel 1 pada sumbu x X2 = letak partikel 2 pada sumbu x X3 = letak partikel 3 pada sumbu x
	y1 = letak partikel 1 pada sumbu y y2 = letak partikel 2 pada sumbu y y3 = letak partikel 3 pada sumbu y
	z1 = letak partikel 1 pada sumbu z z2 = letak partikel 2 pada sumbu z z3 = letak partikel 3 pada sumbu z

kESEIMBANGAN BENDA TEGAR

Jika benda dipengaruhi gaya yang jumlahnya nol ΣF = 0 maka benda akan lembam atau seimbang translasi. Hukum I Newton dapat dikembangkan untuk gerak rotasi. Jika suatu benda dipengaruhi momen gaya yang jumlahnya nol (Στ = 0) maka benda tersebut akan seimbang rotasi.

Kedua syarat di atas itulah yang dapat digunakan untuk menjelaskan mengapa sebuah benda tegar itu seimbang. Sebuah benda tegar akan seimbang jika memenuhi keadaan syarat di atas. Berarti berlaku syarat di bawah.Jika benda dipengaruhi gaya yang jumlahnya nol ΣF = 0 maka benda akan lembam atau seimbang translasi. Hukum I Newton dapat dikembangkan untuk gerak rotasi. Jika suatu benda dipengaruhi momen gaya yang jumlahnya nol (Στ = 0) maka benda tersebut akan seimbang rotasi.

Soal dan Penyelesaian

Sebuah papan panjangnya 2 m diberi penopang tiap-tiap ujungnya seperti pada Gambar. Massa papan 10 kg. Pada jarak 50 cm dari penopang B diletakkan beban 80 N. Jika sistem dalam keadaan seimbang maka tentukan gaya tekan normal yang bekerja di titik A dan B!

Penyelesaian :

Untuk menentukan nilai NA dan NB dapat digunakan syarat persamaan di atas. Karena keduanya belum diketahui, gunakan syarat Στ = 0 terlebih dahulu.

Acuan titik A

Momen gaya yang bekerja dari titik A dapat digambarkan seperti pada Gambar , dan

berlaku syarat berikut.

ΣτA = 0

(AB). NB − (AO). wAB − (AC) . w = 0

2 . NB − 1. 100 − 1,5 . 80 = 0

2 NB = 220

NB = 110 N

Nilai NA dapat ditentukan dengan syarat ΣF = 0 sehingga diperoleh :

ΣF = 0

NA + NB − wAB − w = 0

NA + 110 − 100 − 80 = 0

NA = 70 N

2. Sebuah papan nama bermassa 10 kg digantung pada batang bermassa 4 kg seperti pada Gambar (a). Agar sistem dalam keadaan seimbang maka berapakah tegangan minimum yang dapat ditarik oleh tali BC?

Penyelesaian :

Tegangan T minimum adalah besar tegangan yang dapat menyebabkan sistem itu seimbang sesuai beratnya. Gaya dan momen gayanya dapat
digambarkan seperti pada Gambar (b).
Nilai T dapat ditentukan dengan syarat Στ = 0 di titik A.
ΣτA = 0
(AB).T sin 30O− (AB).wAB−(AB).w = 0
l . T . − l . 40 − l . 100 = 0
T − 40 − 200 = 0
T = 240 N

MOMEN INERSIA

Momen inersia (Satuan SI : kg m²) adalah ukuran kelembaman suatu benda untuk berotasi terhadap porosnya. Besaran ini adalah analog rotasi daripada massa. Momen inersia berperan dalam dinamika rotasi seperti massa dalam dinamika dasar, dan menentukan hubungan antara momentum sudut dan kecepatan sudut, momen gaya dan percepatan sudut, dan beberapa besaran lain. Meskipun pembahasan skalar terhadap momen inersia, pembahasan menggunakan pendekatan tensor memungkinkan analisis sistem yang lebih rumit seperti gerakan giroskopik.

Lambang I dan kadang-kadang juga J biasanya digunakan untuk merujuk kepada momen inersia.

Konsep ini diperkenalkan oleh Euler dalam bukunya a Theoria motus corporum solidorum seu rigidorum pada tahun 1730.^[1] Dalam buku tersebut, dia mengupas momen inersia dan banyak konsep terkait.

Definisi sederhana momen inersia (terhadap sumbu rotasi tertentu) darisembarang objek, baik massa titik atau struktur tiga dimensi, diberikan oleh rumus:

di mana m adalah massa dan r adalah jarak tegak lurus terhadap sumbu rotasi.
 

Analisis

Momen inersia (skalar) sebuah massa titik yang berputar pada sumbu yang diketahui didefinisikan oleh

Momen inersia adalah aditif. Jadi, untuk sebuah benda tegar yang terdiri atas N massa titik mi dengan jarak ri terhadap sumbu rotasi, momen inersia total sama dengan jumlah momen inersia semua massa titik:

   

Untuk benda pejal yang dideskripsikan oleh fungsi kerapatan massa ρ(r), momen inersia terhadap sumbu tertentu dapat dihitung dengan mengintegralkan kuadrat jarak terhadap sumbu rotasi, dikalikan dengan kerapatan massa pada suatu titik di benda tersebut:

   

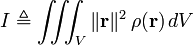
di mana

    V adalah volume yang ditempati objek
    ρ adalah fungsi kerapatan spasial objek
    r = (r,θ,φ), (x,y,z), atau (r,θ,z) adalah vektor (tegaklurus terhadap sumbu rotasi)antara sumbu rotasi dan titik di benda tersebut.

Berdasarkan analisis dimensi saja, momen inersia sebuah objek bukan titik haruslah mengambil bentuk:

di mana

    M adalah massa
    R adalah jari-jari objek dari pusat massa (dalam beberapa kasus, panjang objek yangdigunakan)
    k adalah konstanta tidak berdimensi yang dinamakan "konstanta inersia", yangberbeda-beda tergantung pada objek terkait.

Konstanta inersia digunakan untuk memperhitungkan perbedaan letak massa daripusat rotasi. Contoh:

    * k = 1, cincin tipis atau silinder tipis di sekeliling pusat
    * k = 2/5, bola pejal di sekitar pusat
    * k = 1/2, silinder atau piringan pejal di sekitar pusat.

MOMENTUM LINIER DAN ANGULER

MOMENTUM LINEAR

          Untuk sebuah partikel dengan massa m dan bergerak dengan kecepatan v, didefinikan mempunyai momentum :

                                      p = m v.

Untuk n buah partikel, yang masing, masing dengan momentum p₁, p₂ , ... ,  p_n, secara kesuluruhan mempunyai momentum P,

                            

                                      P = p₁ + p₂ + ... +  p_n

                                      P = m₁v₁ + m₂v₂ + ...  + m_n v_n

                  

                                      P = M v_pm

“Momentum total sistem partikel sama dengan perkalian massa total sistem partikel dengan kecepatan pusat massanya”.

                                     

                                      dP/dt = d(Mv_pm)/dt

                                                   = M dv_pm/dt

                                      dP/dt = M a_pm

Jadi

                                      F_eks = dP/dt

KEKEKALAN MOMENTUM LINEAR

Jika jumlah semua gaya eksternal sama dengan nol maka,

                                      dP/dt = 0

atau

                                      P = konstan

Bila momentul total sistem P = p₁ + p₂ + ... +  p_n, maka

         

                                      p₁ + p₂ + ... +  p_n = konstanta = P₀

Momentum masing-masing partikel dapat berubah, tetapi momentum  sistem tetap konstan.

MOMENTUM ANGULER (SUDUT)

Momentum sudut adalah sebuah besaran fisika yang penting, khususnya untuk masalah-masalah pada tingkat energi dan spektra atom dan molekul. Dalam bagian ini, momentum sudut akan didefinisikan dan sifat-sifatnya akan dijelaskan.

Momentum sudut dari sebuah partikel didefinisikan sebagai sebuah produk luar (produk vektor) r x p dari posisi vektor r yang menyatakan posisi (x, y, z) dan momentum  = (x, y, z).

(1.96)

Persamaan ini dapat ditulis ulang dengan komponen-komponen berikut.

(1.97)

Momentum sudut yang diperkenalkan di sini disebut sebagai momentum sudut orbital karena ini berkaitan dengan gerak orbital klasik dari partikel.